Rakendades matemaatikat erinevates valdkondades
Avaldaja:Merje Pors26. Mai 2014
matemaatika, lai kursus, riina timmermann, gustav adolfi gümnaasium
Millal kasutada üht, millal teist taksot? Kas pikematel inimestel on ka luud pikemad? Neid ja teisi elulisi ülesandeid saab lahendada gümnaasiumi laia matemaatika ainekava 14. kursuse jooksul.
Gustav Adolfi gümnaasiumi matemaatikaõpetaja Riina Timmermann kirjutab gümnaasiumi laia matemaatika ainekava 14. kursuse materjalidest enda kui tegevõpetaja ja ühe materjali looja pilgu läbi.
Kursuse materjalide hulgas on üheksa teemat ja püüan siin välja tuua need ülesanded või projektid, mida on kindlasti võimalik kasutada gümnaasiumiprogrammi kordamiseks, lõimimiseks teiste valdkondadega ja seostamiseks igapäevaeluga.
Kõik kursuse materjalid on õpetajale kättesaadavad Hariduse Infotehnoloogia Sihtasutuse (HITSA) Moodle’i e-õppe keskkonnas üldhariduskoolide kategoorias „Gümnaasiumi valikkursused”. Kõigile on kättesaadav õpik (125 lk) Koolielus.
Gümnaasiumi 14. kursuse „Matemaatika rakendused, reaalsete protsesside uurimine“ õppeeesmärgiks on tutvustada matemaatika rakendusi erinevates valdkondades (bioloogia, füüsika, geograafia, keskkond, majandus, muusika, sport, tehnoloogia, tervishoid) ja anda oskusi lihtsamate reaalseid nähtusi kirjeldavate matemaatiliste mudelite loomiseks, nende analüüsimiseks ja tõlgendamiseks.
Põhiliselt kasutatakse lineaar-, ruut- ja eksponentfunktsioonidel põhinevaid matemaatilisi mudeleid. Pärast kursuse läbimist mõistab õpilane ümbritsevas maailmas valitsevaid loogilisi, funktsionaalseid ja statistilisi seoseid, oskab erinevates eluvaldkondades rakendada matemaatilisi meetodeid, esitada igapäevaelu probleemi matemaatika keeles ning interpreteerida ja kriitiliselt hinnata matemaatilisi mudeleid igapäevaelu kontekstis.
Õppekomplekti kuuluvad õpik, töölehed, lahendusi ja metoodilisi soovitusi sisaldav õpetajaraamat, interaktiivsed demod, testid õpikeskkonnas Moodle, ekraanivideod ja muud elektroonsed lisamaterjalid. Õppekomplekt asub Moodle´i õpikeskkonnas ja paberkandjal seda trükitud ei ole.
Eluliste ülesannete lahendamine
Kursusel on suur rõhk asetatud eluliste ülesannete lahendamisele. Ülesanded on mõeldud nii auditoorseks kui ka koduseks lahendamiseks, kasutada tuleb nii paberit-pliiatsit ja kalkulaatorit kui ka arvutit. Mitmete teemade läbimiseks soovitatakse kasutada aktiivõppe meetodeid (paaris- või rühmatöö, avastamine, suhtlemine ja koostöö, enda ja teiste töö hindamine jne).
Tegevõpetajana hindan ekraanivideoid ja õpetajaid aitavaid töö- ja lahenduslehti (õpetajate materjalide hulgas), mis abistavad ja juhendavad tunni läbiviimist ja õpilaste tulemuste kontrollimist. Samuti on kasulik õpetajaraamat, kus on teemade jaotus ja ülesannete lahendused ning vastused. Õpilaste teadmiste hindamiseks on pakutud auditoorset kontrolltööd (2 varianti koos lahenduste ja hindamisjuhistega), kodust kontrolltööd, enesekontrolli teste, projekte, rühmatöid. Kuna matemaatikat on püütud lõimida väga erinevate valdkondadega, milles matemaatikaõpetaja ei pruugi pädev olla, on Moodle´i õpikeskkonnas lisaks linke ja viiteid erinevate teemade kohta. Ka õpilastele on need kättesaadavad ja täiendavaks materjaliks.
Tegemist on väga kaasaegse materjaliga, sest mõeldud on juba sellele, et õppetöös kasutatakse tahvelarvuteid, nutiseadmeid. Seega puudub vajadus paberkandjal õpiku järele. Kõik tööülesanded, videod ja simulatsioonid avanevad neis seadmetes. Sellega avaneb võimalus anda tund tavalises klassiruumis, mitte arvutiklassis.
Kursuse plussid:
Palju mitmekülgset materjali, õpik õpilastele, õpetajaraamat, töölehed õpilastele, projektide kirjeldused ja juhised, huvitavad demod, ekraanivideod, mitmekesised ja huvitavad simulatsioonid, lisamaterjalid, veebilingid, enesekontrolli testid, kontrolltööde näidised, õpetajale abimaterjalid (töölehtede lahendused), elulised ülesanded ja projektid.
Kursuse miinused:
Aeg: viimane kursus enne eksamit, vaja korrata. Samuti on arvutiklassid ülekoormatud, seal ka raske tundi läbi viia (nt 36 õpilasega), arvutiklassidel on erinev tase (riistvara) ja Moodle´it ei ole koolides piisavalt kasutatud.
Jään optimistlikuks ja arvan, et igasugused probleemid arvutiklassides oleva riistvara ja tarkvaraga leiavad lahenduse. Ning kindlasti annab õpetajatele kindlustunde, kui osaleda tasuta TTÜ poolt pakutavatel koolitustel.
Kursusel käsitletakse üheksat teemat ja püüan siin välja tuua need ülesanded või projektid, mida kindlasti on võimalik kasutada gümnaasiumiprogrammi kordamiseks, lõimimiseks teiste valdkondadega ja seostamiseks igapäevaeluga.
1. Mis on mudel?
Mudeli kasutamine.
Pimedas ilma helkurita teel liikuvat jalakäijat näeb lähituledega sõitva auto juht 30 meetri
kauguselt. Helkuriga jalakäija on nähtav 130 meetri kauguselt.
Milline võib olla auto kiirus, et juht ei sõidaks otsa ootamatult nähtavale ilmunud jalakäijale,
kui a) jalakäija ei kanna helkurit?
b) jalakäija kannab helkurit?
2. Õpime tõlkima: mudeli verbaalne ja matemaatiline kuju.
Kodune ülesanne: pere ööpäevase vee tarbimise määramine.
Eesmärgiks on oma pere keskmise ööpäevase vee tarbimise määramine. Kõikide õpilaste
poolt kogutud andmeid kasutatakse hiljem vee tarbimise mudeli analüüsimisel.
3. Konstantne muutumine ja lineaarsed mudelid.
Autod teel.
Rühmatöö teema: ühtlase liikumise liikumisgraafikute analüüs.
Seitse erinevat värvi autot asuvad maanteel ühe ristmiku lähedal. Joonisel on toodud nende
liikumisgraafikud. Graafikuid uurides tuleb kindlaks teha iga auto liikumise suund, asukoht ja
kiirus ristmiku ning teiste autode suhtes.
Kujutage ette, et istute mitmekesi väljavalitud autos. Mida te näete oma reisi järgmise 15
sekundi jooksul? Millal ja kuskohast te alustasite oma sõitu, milline on teie auto kiirus ja mis
toimub teie ümber — mida te näete selle aja jooksul ees, tahavaatepeeglist ja küljeaknast,
mida teevad teised autod, milline on nende kiirus teie suhtes?
Arutleda omavahel, teha märkmeid ja valmistuda analüüsi ettekandmiseks.
4. Kuidas leida parimat sirget?
Küünarvarre ja keha pikkus.
Rühma- ja individuaalne töö.
Vajalikud vahendid: mõõdulint, joonlaud.
Kas pikematel inimestel on ka luud pikemad? On loogiline arvata, et inimese keha pikkus on seotud tema luude pikkusega. Seda seost kasutavad näiteks arheoloogid, kes väljakaevamistel leitud luude põhjal teevad järeldusi seal elanud inimeste pikkuse kohta. Samuti kasutatakse seda seost kriminaalantropoloogias (antropoloogia on teadus, mis uurib inimese kehalisi iseärasusi ja inimeste eellaste kujunemist).
Oletame, et kriminalistid leiavad inimesele kuuluvad luud, millest vaid osa on säilinud. Antropoloog suudab kindlaks teha, mis sugu see isik oli, kui pikk ja kui vana. Selleks on vaja aga eelnevalt konstrueerida mudelid, mis näiteks skeleti erinevate osade põhjal võivad prognoosida inimese pikkust.
Eesmärgiks on koostada mudel, mis küünarvarre pikkuse alusel võimaldab prognoosida keha pikkust.
5. Tõus ja langus: paraboolsed mudelid.
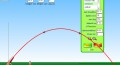
Optimaalse heitenurga leidmine.
Õpilased peavad analüüsima, millise heitenurga korral on keha lennukaugus maksimaalne.
Selleks tuleb läbi viia katsed erinevate heitenurkade korral, kahe erineva algkiiruse ning
õhutakistuse puudumise ja olemasolu korral. Õpilased võivad valida erinevad kehad ja tunni
lõpus saab võrrelda, kas tulemus on erinevate kehade korral ühesugune või mitte.
6. Kas maailmas jätkub ressursse? Eksponentsiaalne ja logistiline kasv.
Kui bakter pooldub iga 20 minuti tagant, siis kui palju on baktereid 24 tunni pärast?
7. Võta või jäta.
Millal kasutada üht, millal teist taksot?
Takso A korral on sõidu alustamistasu 1,98 eurot ja kilomeetri hind 0,48 eurot. Takso B korral on sõidu alustamistasu 2,7 eurot ja kilomeetri hind 0,33 eurot. Millal tuleks eelistada taksot A ja millal taksot B?
Lahendada kahel viisil: geomeetriliselt programmiga GeoGebra ja algebraliselt.
8. Muusika, matemaatika ja siinus.
Harmooniline võnkumine on võnkumine, mida saab kirjeldada siinusfunktsiooni või koosinusfunktsiooni abil.
9. Agendid mudelis.
a) Mudel simuleerib metsatulekahju levikut. Tulekahju algab metsa vasakust servast ja levib igas neljas suunas. Selgub, et see, kas tuli jõuab metsa teise serva, sõltub sellest, kui tihedalt puud kasvavad. Mudelis eeldatakse, et tuult ei ole tuli saab levida vaid sinna, kus kasvavad puud (ei saa kaugele hüpata).
b) Mudel simuleerib HIV viiruse levikut väikeses isoleeritud inimpopulatsioonis ja analüüsib seksuaalkäitumise mõju viiruse levikule. Mudeli abil saab uurida, kuidas mõjutavad HIVi levikut neli tegurit, mis iseloomustavad vaadeldavat inimpopulatsiooni:
• seksuaalelu aktiivsus;
• keskmine aeg, mille jooksul partnerit ei vahetata;
• kondoomi kasutamise harjumus;
• HIV testimise sagedus.
Neid nelja parameetrit saab muuta ja analüüsida HIV leviku kiiruse sõltuvust nendest. Õpilastele on ette antud soovitused, milliste eespool nimetatud parameetrite väärtustega nad peavad mudelit analüüsima.
Kokkuvõtteks võiks öelda, et kes ei proovi see ei tea. Pealehakkamine on pool võitu. Põnevat avastamist!
Autor: Gustav Adolfi gümnaasiumi õpetaja Riina Timmermann
Samal teemal: